What were the big ideas?

The main ideas presented in week two’s lecture related to the skill of addition. This lecture also extends on the definition of mathematics by further emphasizing the importance of ‘recognising, exploring, extending, representing, and understanding patterns and relationships’ to help students recognise and use this language more frequently during their time in school. 

My understanding of the weekly topic has changed as I now understand the importance of demonstrating breaking down sums to portray more than a symbol and by doing this students can gain a better understanding and conceptualisation of these mathematical ideas through the use of more appropriate language and creative resources.

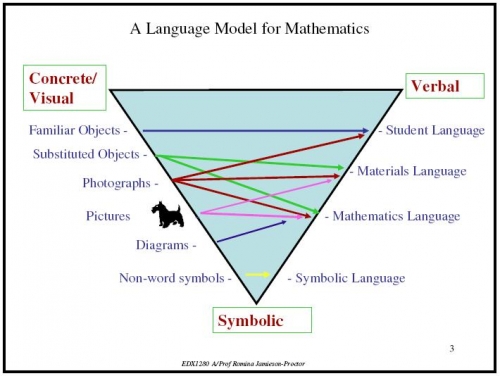
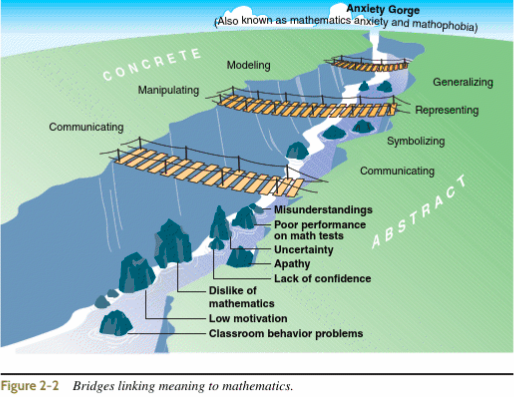
The previously listed understandings will shape my future teaching abilities as I will teach the concepts, skills and strategies involving Addition by utilising The Language Model, to more efficiently move students through the four stages from concrete and verbal, to eventually symbolic being the final goal. Keeping in mind that all children learn at different rates.

Addition: concept, skill or strategy

The Addition concept can be simplified and explained as the joining of groups together to find a total. This concept is usually first introduced in the foundation to year 1 of schooling. Just like most other mathematical concepts when teaching addition the language model containing 4 stages needs to be taken into consideration . Students must PHYSICALLY move things together to develop the understanding in their head (Jamieson-Proctor & Larkin, 2012).

Misconceptions

One of the main misconceptions relating to Addition is the thought that when numbers are added together that the final answer is always larger however, this is not the case. As students in primary school progress to solving higher levels mathematical equations that involve addition this thought may lead to confusion. When dealing with negative numbers, the answer is not always larger.

To avoid students developing this misconception during lessons I would focus more on  teaching for understanding and allow students to gain deeper conceptualisation, by including more creative activities when dealing with problem-solving.

ACARA

Addition within mathematics is first introduced within the Australian Curriculum in the foundation year. (ACARA, v8.3).

Mathematics/ Foundation Year/ Number and Algebra/ Number and place value/ ACMNA004

Scootle Resource

Addition and subtraction level 1: numbers to 5 is a registered Scootle resource/activity that can easily be used for young children ranging from the foundation year to grade 2. Students are required to read simple word problems and find the tile matching the answer description or total it equals to. For example, two groups that make 4 together?. This particular activity provides an engaging opportunity for students to explore and realise how useful it is to solve addition problems. It also clearly communicates the connection between worded problems, symbols and simple equations.

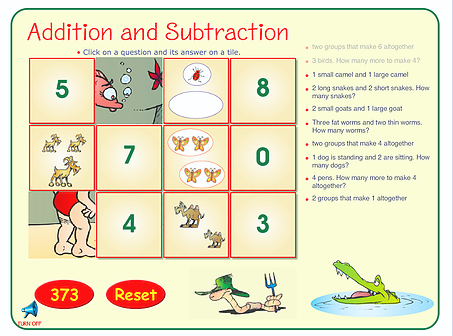
Screenshots of the game all retireved from https://worksheets.mathsbuilder.com.au/games/selector/Addition_and_Subtraction/0/

This resource would be appropriate to use at the mathematical language stage as it uses a good combination of visual graphics and word problems.

Resources or Teaching Strategies

This is an addition mat. It is used to demonstrate the concept of addition in early primary classrooms. I am intrigued by the use of these clever addition mats when teaching lesson in early mathematical concepts. This resource allows children to see physical representations of numbers and how they can be brought together to cretae a total, while assisting in the strategy of counting on. This resource would also be an engaging way to personalise the lerning for some children with additional needs as it be changed to suit different interests. e.g. an autistic  child with a very strong interest in planes.

Textbook: Concept, skill or strategy

In chapter 11, Reys discusses the evolution of teaching strategies and older methods for teaching mathematical equations such as using paper-and-pencil procedures (or computational algorithms ) and how they were once considered an essential component for teaching. However, he then proceeds to explain that this has since been outdated and through research new methods have been discovered and implemented in many classrooms. The focus has shifted to what the students themselves construct or develop through making meaningful connections. Students are now encouraged to share their way towards solutions, justify their thinking and communicate their findings. The tradition of once having to memorise procedures given by the teacher or mentor, without concrete understanding is not the preferred approach (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11751&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2019). Scootle. Retrieved May 7, 2019, from http://www.scootle.edu.au/ec/p/home

Jamieson-Proctor, R., & Larkin, K. (2012). “Mathematics as a Language”: A Theoretical Framework for Scaffolding Students’ Mathematical Understanding. Retrieved from https://leo.acu.edu.au/pluginfile.php/3070058/mod_book/chapter/189986/Maths%20Language%20Model.pdf

Maths Builder. (2011). On Your Mark Mathematics. Retrieved from https://worksheets.mathsbuilder.com.au/games/selector/Addition_and_Subtraction/0/

Mikkelsen, P. (2013, May 8). Addition Mat [Video file]. Retrieved from https://youtu.be/H9knavDn5lQ

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy2.acu.edu.au

What were the big ideas?

The main ideas presented in lecture one related to the definition of what mathematics is and how everything could be related back to the conceptual language model for teaching and learning mathematics. This was then followed by a discussion about the negative culture and stereotypes surrounding the subject. As someone who struggled with maths in the past, I found this very interesting because I have always found these concepts very foreign myself during my time in school.

Personal Impact

Being someone who struggled with grasping mathematical concepts in the past, I found this very interesting because I have always found these concepts very foreign myself during my time in school. As an individual seeking to enter the teaching industry in the future, I will make more of an effort to ensure students are not filled with negative thoughts or assumptions about mathematics. Instead, I will aim to demonstrate and explain various practical ways these skills I am teaching them can be applied in their everyday lives outside of the classroom. 

Supporting Sources

In their research paper Learning And Fearing Mathematics:
Insights from Psychology And Neuroscience, Booker and Reid refers to these negative connotations surrounding mathematics and goes into further detail about the consequences for these being present in the classroom. Throughout the article, these negative emotions demonstrated by students are labeled as a “barrier to developing mathematical proficiency”. (Buckley and Reid, 2013).

The Language Model Concept

By following the language model for mathematics as a guide, I can assist students in understanding maths in an engaging way. By incorporating activities such as the use of addition mats and MAB blocks. Because the concept of mathematics is first introduced to young students during the foundation year of school I will introduce it to them using visual and hands-on methods, uncomplicated and clear language and the previously listed resources.

After the students demonstrate a solid understanding I will continue to slowly introduce more specific mathematical materials and language such as songs and sums with supportive pictures. Only when the children are completely ready will I consider introducing the abstract mathematical symbols such as plus + minus – and multiply x. By doing this it will also give younger students the ability to relate present day school mathematics to real-life situations around them (Burnett & Wichman, 1997).

The language model diagram below shows the teaching sequence for most mathematical skills taught in the classroom.

Misconceptions

According to ORIGO Education reported by eSchool News, Common misconceptions can cloud a child’s early math judgment so it has become very important to educate teachers on how to avoid teaching them by mistake and how to overcome them. these mistakes in teaching can hinder the learning of basic number concepts and operations that are considered important for developing early math skills. It was often because there are many words (and symbols)with multiple meanings, and students have confused one word or symbol for another with a different meaning (Pierce, 2017).

For Example, the number words “one,” “two,” “four,” and “eight” all have commonly known homonyms: won, to, for, and ate.

Personal Resources

There are already a lot of games on the accessible to the public that claim to assist everyday people in teaching math. For example some that I have at home include Snakes and Ladders which manages to introduce young children to numbers 1 through to 100 in a creative and engaging way.  Monopoly is another good one for older age groups for addition, subtraction and introducing the value of money. By using these resources maths can become an activity they looking forward to rather than a repetitve drill.

Digital Tool

I have chosen to display my portfolio of the next 12 weeks on WordPress as it allows me to express myself more visually while being creative with how I want to learn and refer back to content. This was also a bit part of week one’s tutorial. It would be wrong of me to expect my future students to be engaged in a subject that I myself am not enthusiastic about or interested in.

Textbook Source

Reys et al., chapter 2, figure 2.2 shows a diagram that demonstrtes an emphasis of meaning and understanding mathematical concepts rather than memorization. Children attempting to or being taught to memorize these concepts or skills without understanding are likely to fall into the “anxiety gorge”. Assissting students to make clearer connections between the concrete (e.g., models and manipulatives) and the abstract (e.g., generalizations and symbolic representations) helps understanding, promotes successful learning, and helps relieve the anxiety that seems to surround mathematics.

Modeling problem-solving strategies rather than presenting student with finished solutions helps them to realise that using incorrect strategies and taking numerous unnecessary steps are a natural part of developing these skills.

References

Buckley S., & Reid K. (2013). Learning And Fearing Mathematics: insights from Psychology And Neuroscience. Retrieved from https://leo.acu.edu.au/pluginfile.php/3070063/mod_resource/content/1/Learning%20and%20fearing%20mathematics.pdf

Burnett, S. and Wichman, A. (1997). Mathematics and literature: An approach to                        success. Chicago, IL: Saint Xavier University.

Pierce, D. (2017, August 22). The 4 simple misconceptions that can derail early math education. Retrieved from https://www.eschoolnews.com/2017/08/24/misconceptions-early-math-ed/