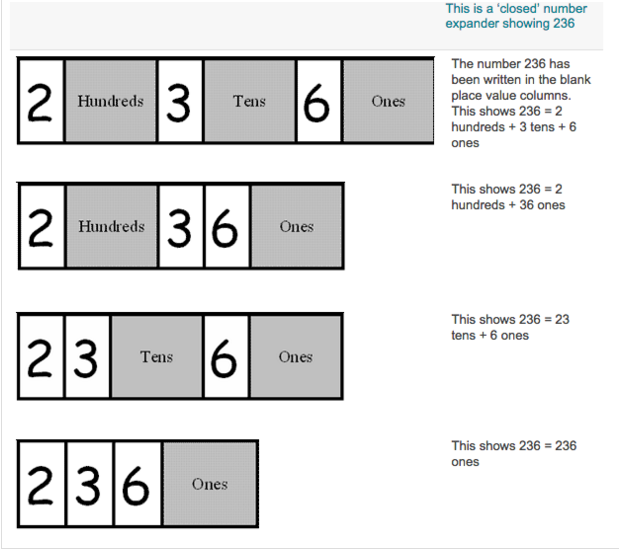
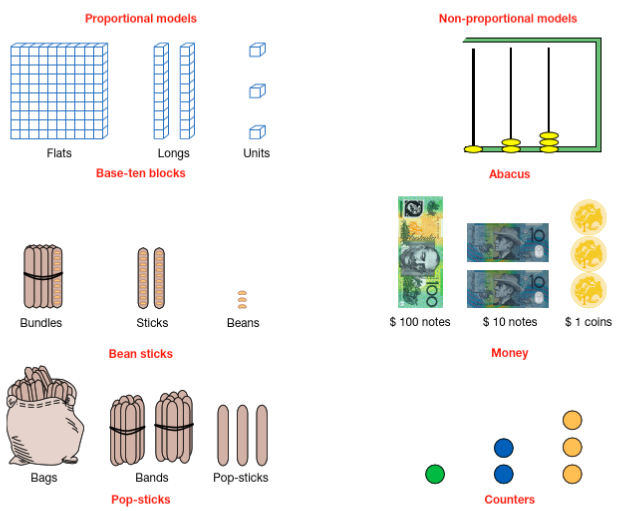
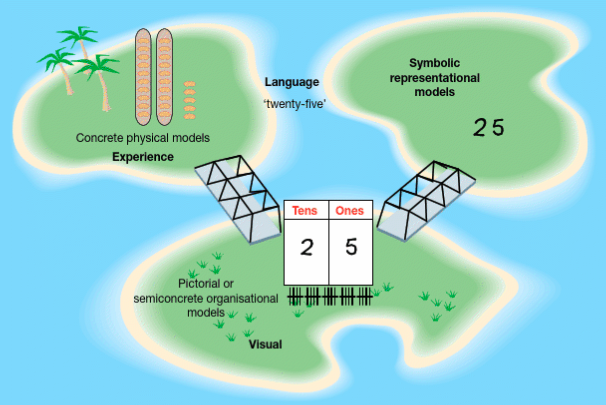
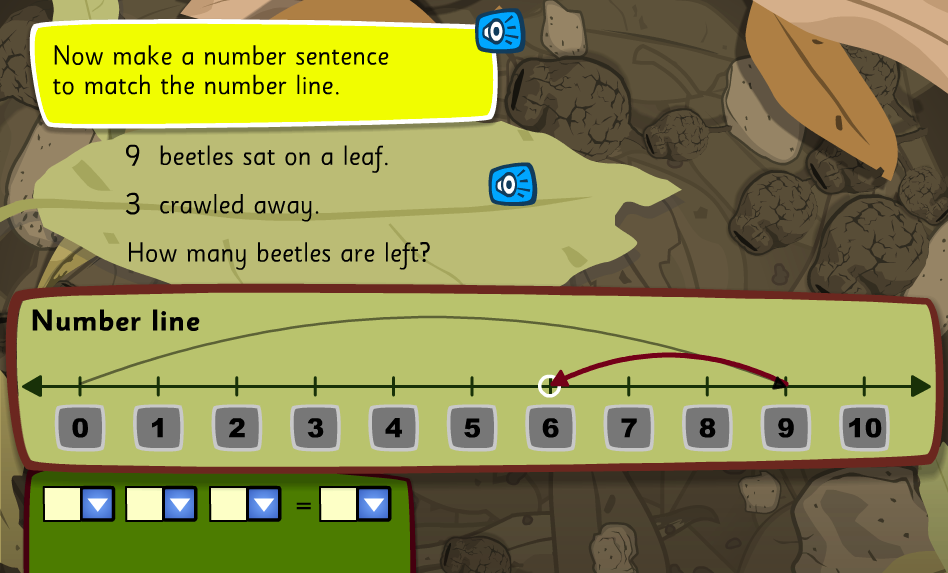
What were the big ideas?

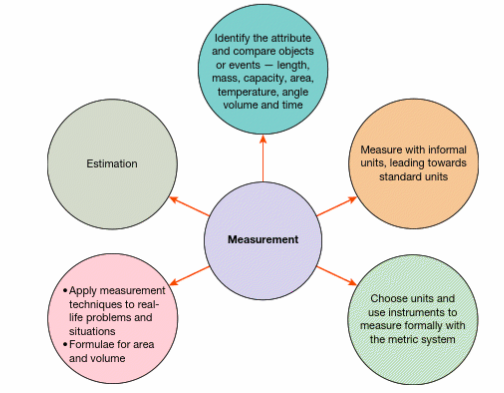
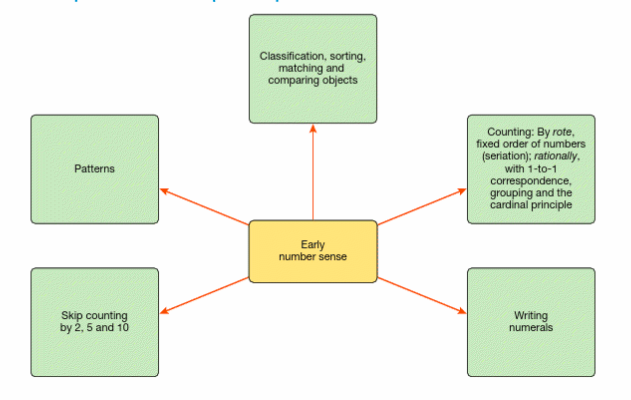
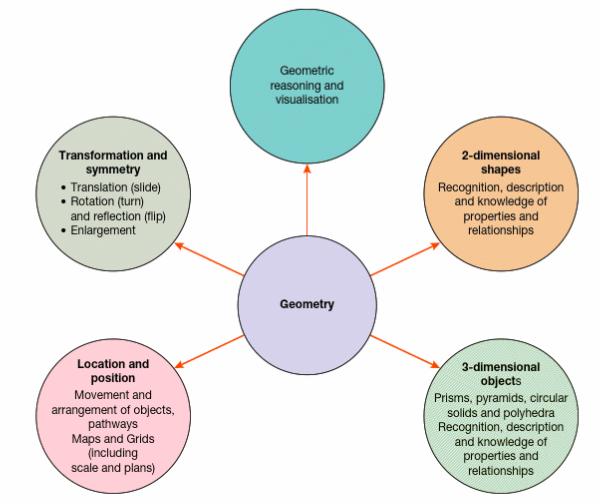
The big ideas from this week involved looking at the concept of Geometry. Initially I was under the impression that geometry was specifically the learning of shapes and their properties. However, after this weeks lessons I now know through demonstrations that the concept of geometry involves a study of shape, space and also measurement (Jameson-Proctor, 2019). This directly links to the week 11 Measurement content as students often need measure the perimeter or area of shapes or their various angles, sides, faces or vertices. 

Before students start learning geometry, they first need to physically engage and experience the attributes of shapes for themselves and know how they are involved in our everyday lives. Only after this prior knowledge can students start solving formulas.

My personal understanding of this weeks topic has significantly changed as I have learnt about the importance geometry has in our everyday lives and students should be presented with more oportunities to apply their geometric knowledge beyond traditional classroom settings. Because of these new understandings, in the future I will make sure I utilise things like cognitive development, sensorimotor stage and the concrete stage so students can make meaning of geometry.

Geometry: one concept, skill or strategy

There are many skills involved with the concept of geometry, one of which is being able to visually draw and model different shapes. This skill involves an already sound understanding of geometry, and is the third skill in the “5 Basic Skills of Geometry.” Because of this, students must have previously communicated the attributes and relationships of shapes.

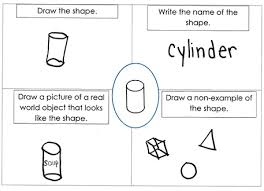
This skill involves the student being able to sketch and draw 1D, 2D and 3D shapes to scale while using materials such as cardboard, blocks and clay to model these shapes in fun and different ways (Jameson-Proctor, 2019). Informal shape constructions such as “Nets” which is folding paper to create a shape should be explored before the more formal introduction of technologies like protractors and compasses. This particular skill would usually be introduced whenmost students are at the materials and mathematics stage of the language model. This is mainly because it involves introducing mathematical materials and language that relate to geometry.

Misconceptions

A common geometry misconception that students can have when first learning this concept is that a prism and a pyramid are the same thing. This misconception is oftenly formed between the pyramid and the triangular-based prism.

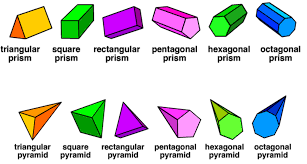
This misconception is more likely to occur when students have not quite understood the specific attributes of prisms and pyramids , or they do not understand that the different names mean that these two shapes have different attributes.

In order to stop this misconception from developing I would start by taking students  back to the children and materials language stage of the model. This is so they can link the shapes again with real experience and examples (such as the egyptian pyramids). When revisiting these two particular shapes, It is the teachers job to discuss the attributes of these shapes while getting students to model, draw and create “nets” of them. This will allow students to recognise the difference and explain that a pyramid has a base with triangular faces reaching up to a point and how the prisms has a base, together with a translated copy of it.

ACARA

Geometry is first introduced in the foundation year, for students within the Australian Curriculum, Assessment and Reporting Authority (ACARA, 2017)

Mathematics/ Foundation Year/ Measurement and Geometry/ Shape/ ACMMG009

Scootle Resource

Shape sorter: Basic Shapes is a Scootle resource that can help students compare shape features in order to identify the geometric properties that define a set of shapes. (Education Services Australia, 2013). In this game students must help sort single or pairs of given shapes. This resource was recommended for students in Year 5 as it may be to advanced to align with the foundation year curriculum (ACMMG009) where students are required to sort and describe shapes in their environment.

All Screenshots for this game were retrieved from: http://www.scootle.edu.au/ec/viewing/L8163/index.html

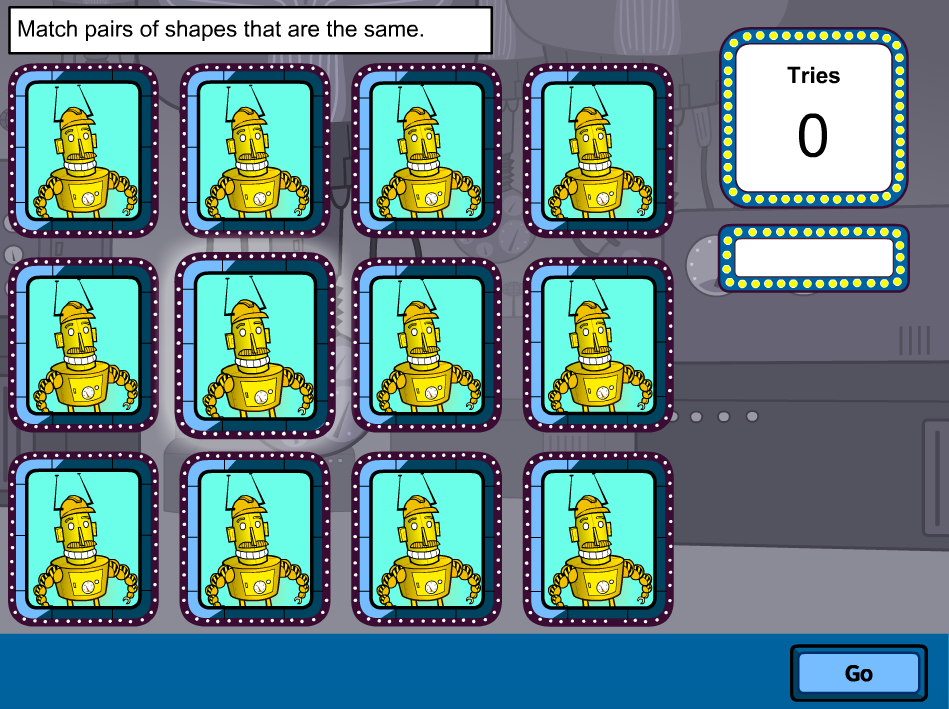
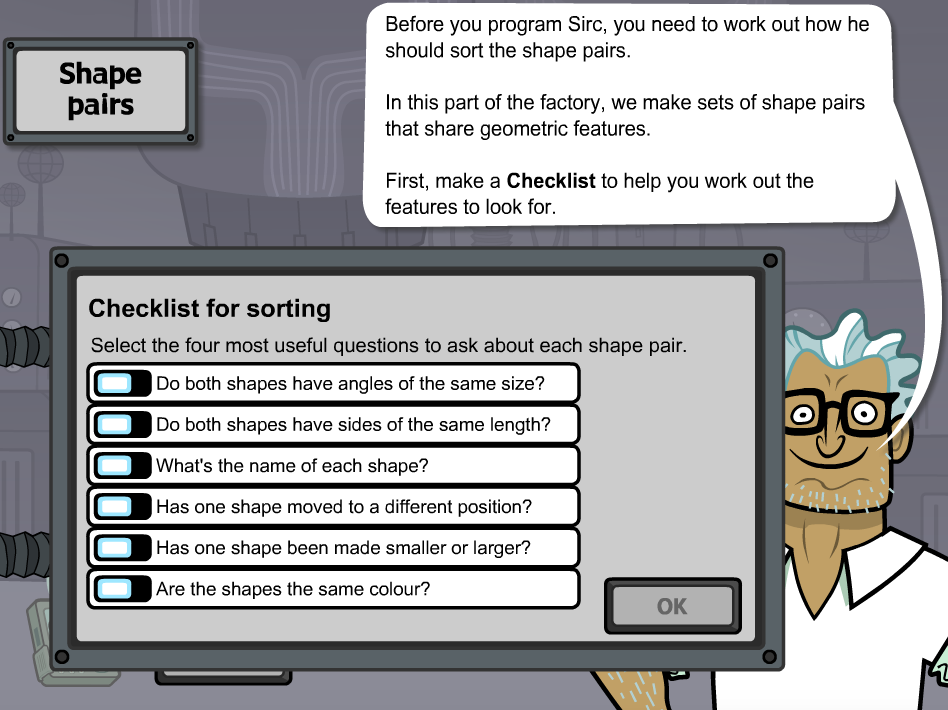
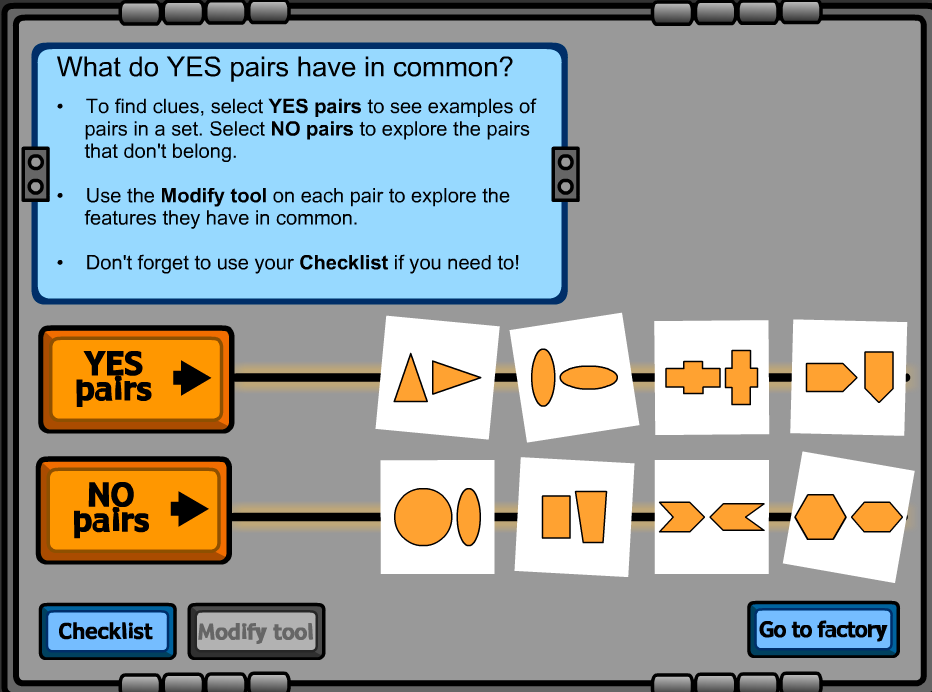
This would be used when children are at the mathematics language stage as they use language such as length and geometric. In this particular resource they do not point out the names of the shapes students will be presented with, therefore students would have to already know that names of the shapes. This may potentially limit some students if they don’t already have an understanding of these names. Overall, in order for students to fully understand the concept of geometry and how various shapes can be identified by their physical attributes, this interactive game could be easily utilised as a tool to help children visualise and grow their knowledge of shapes.

Resources or teaching strategies

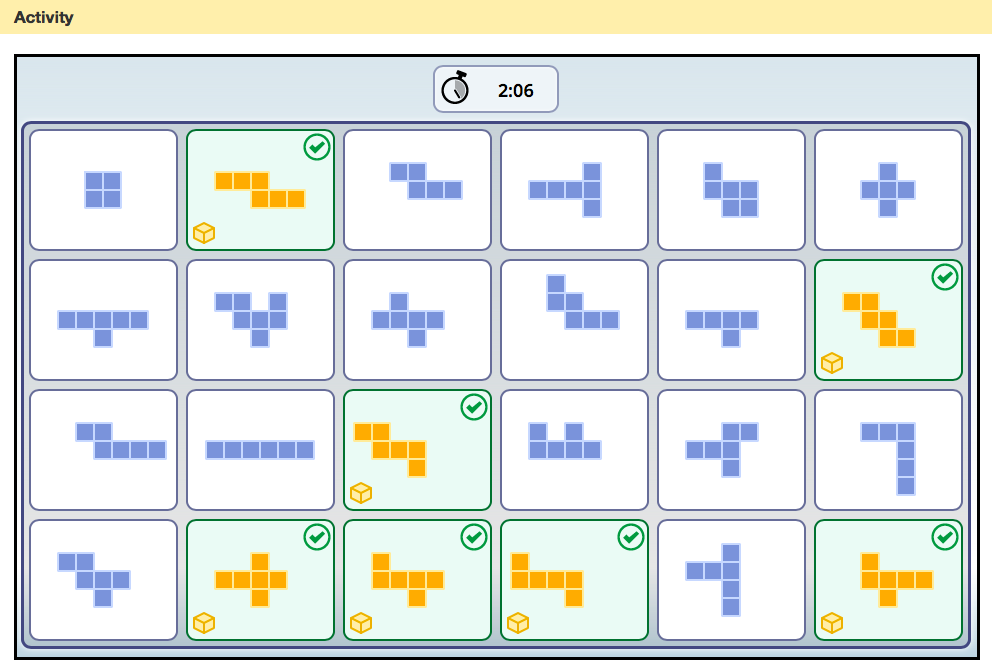
Cube Nets is another online game that recommended for students in year 3 through to year 5. Students can play this in order to test and revisit the number of faces on a cube. This game enables students to identify the different net patterns that could be successfull and ask themselves which of these nets will form a cube? (National Council of Teachers of Mathematics, n.d.). This game would be used for children at the materials language stage.

However, this game does contain some limitations, as students are not physically experiencing these nets in real life. An advantage of utilising a resource like this would be when students don’t personally own some of these nets at home, and this game would provide an easy way to demonstrate this when there is a lack of resources or time to make these in classroom. One final limitation to this game is it only focuses on cube nets, to make this resource more effective creating more similar to it with different shapes would become very useful for teachers.

Textbook : concept, skill or strategy

Reys chapter 16 explains why students are required to be able to describe properties of 3-dimensional objects to explain how 2 or more different objects are alike or different geo­ metrically through comparison (Reys, 2014).

Even though students begin learning describing and sorting are processes in early childhood and it should be continued throughout most of primary school. When students reach higher grades more complex and unfamilliar properties can be added to thier repertoire. These describing and sorting activities can help students develop the ability to think abstract/relational which is an essential skill for high school geometry where more complex responses are required (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11751&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2013). Shape sorter: basic shapes. Retrieved from http://www.scootle.edu.au/ec/viewing/L8163/index.html

Jack Hartmann Kids Music Channel. (2018, April 24). Shapes, Sides and Vertices | Version 1 | Jack Hartmann [Video file]. Retrieved from https://youtu.be/24Uv8Cl5hvI

Jamieson-Proctor, R. (2019). EDMA241/262 Mathematics Learning and Teaching 1: Week 9 Part 1 and 2,  Brisbane, Australia: Australian Catholic University. 

National Council of Teachers of Mathematics. (n.d.). Cube Nets. Retrieved from https://www.nctm.org/Classroom-Resources/Illuminations/Interactives/Cube-Nets/

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au

Scootle. (2019). Home. Retrieved from https://www.scootle.edu.au/ec/p/home

What were the big ideas?

The Big Ideas this week involved looking at the concept of Measurement. This week I have learnt that being able to measure is being able to count in units to record results. However, like most concepts in order for a student to be able to measure correctly they first must have a basic knowledge from week 6 as the connections between this, numbers and counting principles are important.

My personal understanding of this week’s topic has changed as I have learnt that measurement is a topic that contains multiple concepts. Because of these new understanding in the future when teaching I will rememeber to consistently utilise the 4 step teaching sequence as I believe it can help students learn any measurement concept.

Measurement: one concept, skill or strategy

The skill of measuring length in particular is specifically taught through the 4 step teaching sequence. Students even in early primary years should already have formed a conceptual understanding of what length is through prior experiences. In order to begin practicing the skill of measuring length, students use Arbitrary units such as feet, blocks and the length of string to measure the length of an object or to compare these lengths with others in the class. It is recommended that this skill should be done within the first two stages of the language model.

Once students are able to perform this specific skill, they can then be introduced to measuring in the more traditional Standardised units, however, before this they must be taught how to use a ruler or tape measure. Onnly after students have understood how this technology works, they must then use the technology and apply the skill of counting units to correctly measure the length of given objects. A student will be successful at measuring when they can perform the previously discussed skill correctly and the number of units they recorded is correct.

Misconceptions

A common misconception that may occur when students are first learning how to measure length can be when students are using the technology of a ruler. Incorrectly, some students may decide to start measuring at the beginning ‘1 cm’ line, instead of the ‘0 cm’, where the measurement should actually begin. Most of the time this misconception becomes more frequent when students have been shown how to measure with this technology incorrectly or they simply do not understand that the measurement begins at 0 cm.

In an attempt to eliminate this misconeption, I would start by taking the students back to the mathematics language stage where they are introduced to the technology of a ruler of tape measure. They will have to be explained to that there are measurements between 0 centimetres and 1 centimetre, and that unit space is the starting point. In order to physically do this, students could measure small objects like rubbers or small sharpeners to see that there are smaller units that need to be considered, before something can be 1 centimetre long. Teachers could model how there are 10 millimetre that make 1 centimetre, similar to how there are fractional numbers between 0 and 1, therefore, when measuring, even in centimeters we need to consider this.

ACARA

Measuring length is first introduced  in the foundation year, for students within the

Mathematics/ Foundation Year/ Measurement and Geometry/ Using units of measurement/ ACMMG006

Scootle Resource

All screen shots for this resource retrieved from: https://www.funbrain.com/games/measure-it

Measure it is a Scootle recommended for children grades 1 through to 3. This interactive online game provides the option of 3 difficulty levels, it is a requirment that that student is at the symbolic language stage of the resource model to be able to engage with this resource successfully throughout all 3 levels. This particular resource is testing the skill of measuring, as it starts by asking students to choose which measurement they think is the correct answer for where the red line finishes as shown in the picture above (Funbrain Holdings, LLC, 2017). Because students are able to select whether they would like to measure in inches or centimeters students beginning the symbolic stage may use the inches measurement, which could cause misconceptions if they are required to measure in real life, making this a limitation.

Resources or teaching strategies

This teaching resource similar to the first one is an online interactive game that teachers can easily incorporate into math lessons when they are first introducing the idea of comparison. This game could be used for students in foundation year through to year 2. This would be used when children are at the materials language stage of the language model. This game models various comparison questions in an engaging quiz style game. This resource successfully provides an understanding that height is a measurable attribute. All student have to do is select the taller or shorter of two objects using visual comparison (Splash Math, 2019). The only limitation to this resource when compared to the previous is the fact that it doesnt seem to increase in difficulty which could get boring for students that manage to grasp this skill quickly

All screenshots for this resource retrieved from: https://www.splashmath.com/measurement-games

Textbook : concept, skill or strategy

Reys chapter 17 discusses the concept of measurement with multiple examples for all of the measurable attributes. While doing this, Reys also manages to explain the importance of building upon students prior experiences with length, area, volume and capacity, mass, time, temperature and angle, which is the techers given role (Reys, 2014).

In order for a student to measure with understanding, they first need to know what attribute they are supposed to be measuring. For example, younger students may find it more challenging to measure the area of a given object because they might not yet understand the concept of area or surface. However, before this students will gain some intuitive understanding of area from real life experiences, like putting blue coloured paper in their block construction to symbolise a swimming pool (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11751&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2019). Search. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMMG006

Funbrain Holdings, LLC. (2017). Measure It!. Retrieved from https://www.funbrain.com/games/measure-it

KidsEduc – Kids Educational Games. (2015, May 27). Math for Kids: Measurement, “How Do You Measure Up” – Fun & Learning Game for Children [Video file]. Retrieved from https://www.youtube.com/watch?v=zsv7bYSrzMU

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au

Splash Math. (2019). Measurement Games for Kids Online. Retrieved from https://www.splashmath.com/measurement-games

What were the big ideas?

Following on from last week the big ideas of week 10 involve the teaching of Algebra and providing students with multiple opportunities to use this concept when problems solving. Students are more able to easily understand the concept of algebra when they have a good knowledge of the general number properties. Example of these include their additive identity or commutativity (Assessment Resource Banks, 2019).

 Many of the concepts related to algebra are best taught at a younger age because common misconceptions which may develop can inhibit a student’s ability to work with the related symbols later on.  

Algebra: one concept, skill or strategy

In pre algebra, students are often found to struggle with equation solving. In order to provide students with the available the skills and tools that are required for manipulating given equations, students are to be exposed to the suitable algebraic language, notations and reasoning (Van Amerom, 2003).

For instance, older students in grades 6 and 7 are physically able to solve equations at both a formal and an informal level, but when it comes to communicating and providing their reasoning formal symbols thats when tasks become a major obstacle.

Misconceptions

All learners are not blank slates. Each student at the start of a new year brings prior knowledge into a lesson, and that knowledge whether possitive or negative is proven to influence what the student will gain from the experience.

In relation to algebraic problem solving, one main type of prior knowledge that is essential to learning is the conceptual understanding of features involved in the problem. Examples of these include features such as different variables, common or “like” terms and negative signs. Having a conceptual knowledge of these features is not just the ability to recognise these symbols or successfully use them in an operation, but understand why the feature is there an what its purpose is, students should be able to ask themselves “will changing the location of the feature affect the overall problem?” (Booth & Koedinger, n.d). Overall, lack of understanding about these various features will consequently interfere with a students performance when solving equations that involve a specific procedure.

Resources or teaching strategies

All screenshots of the resource retrieved from:

https://www.splashmath.com/algebra-games

Write Expressions is a resource that aims to help students recognise and write algebratic expressions. This resource is particularly aimed at older students in years 5 and 6, as it revisits problem solving skills in order to solve given scenarios. This resource would be introduced to students who are at the symbolic stage of the Algebra language model, as they are already using and understanding the language of repeating, and growing patterns and are able to then expand their knowledge in a more formal and structured way (Splash Math, 2019).

Textbook : concept, skill or strategy

Many primary mathematics curricula include the use of equations to solve routine problems but what they dont know is they fail to emphasis helping students realise where these equations come from and how they make mathematical sense (Reys, 2014). Reys chapter 15 describes how non-routine algebratic problems can be easily represented to students through picturea and other modelling methods. By utilising these non-routine algebratic problems teachers can provide students with various opportunities to perform the skill of analysing number patterns and continuing the pattern (Reys, 2014).

References

Assessment Resource Banks. (2019). Algebraic thinking concept map. Retrieved from https://arbs.nzcer.org.nz/algebraic-thinking-concept-map#introduction

Booth, J., & Koedinger, K. (n.d.). Key Misconceptions in Algebraic Problem Solving. Retrieved from https://pdfs.semanticscholar.org/ebcd/e07919d049b73d44702c549b8c1aa71683e5.pdf

Math Antics. (2015, May 22). Algebra Basics: What Is Algebra? – Math Antics [Video file]. Retrieved from https://youtu.be/NybHckSEQBI

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy2.acu.edu.au

Splash Math. (2019). Algebra Games for Kids Online. Retrieved from https://www.splashmath.com/algebra-games

Van Amerom, B. A. (2003). Focusing on informal strategies when linking arithmetic to early algebra. Educational Studies in Mathematics, 54(1), 63-75. doi:10.1023/b:educ.0000005237.72281.bf

What were the big ideas?

The big ideas from this week following on from week 7 included a more of a focus on how to teach number and place value. I also learnt about the relationships involved with related resource that will help assist this while making lessons engaging.

Number and Place Value: one concept, skill or strategy

During the first 3 years of school, is when students start to investigate Place Value additively as they discover the values of the digits. It is recommended that they investigate both standard and non-standard additive place value types, while being able to describe numbers in place values flexibly (A Learning Place, n.d). They usethis new found understanding to complete tasks such as adding and subtracting single-digit, tens and two-digit numbers using place value methods. 

From Year 3 onwards, students continue to investigate standard and non-standard place value of larger numbers and number that include decimals. Using this understanding they start to add and subtract or multiply and divide, larger whole numbers and decimals using these standard and non-standard additive place value and multiplicative place value methods (A Learning Place, n.d). 

Misconceptions

Misconcepetions in place value may develop for a variety of reasons. They may be due to lack of knowledge or a previous misunderstanding. Some place value misconceptions can be predicted prior to a lesson and tackled at the planning stage to diffuse, or prevent misconceptions from becoming more frequent throughout the rest of the class.

In order to do this, the teacher needs to have the knowledge of why these misconceptions may have occurred. Many of the mistakes that students make with place value written algorithms are due to their misconceptions of basic earlier operations from weeks 2-5 content.

Resources or teaching strategies

Number expanders are easily made by folding strips of paper. Students can enjoy the given challenge of being able to fold them correctly in a fan pattern. Number expanders contain blank spaces next to the written word of each place value as shown above, giving students the chance to add their own numbers . This teaching resource is used to demonstrate the concept of place value and help students gain a visual understanding of place holding within the place value system.

Textbook : concept, skill or strategy

Rey chapter 8 Extending number sense: place value explains that students require a great deal of active experience with making quantities; composing and decomposing numbers; recording multi-digit numbers and connecting models, pictures and symbols in their primary school years (Reys, 2014). The learning of ths particular topic cannot be rushed as it might lead to further misconceptions and a close dependence on mathematical meaning the concept will never be fully understood.

Later confusion as students get older with the four main operations, decimals and measurement has proven to be often linked with inadequate place value understanding not enough practice with different modelling methods. Also, important skills such as estimation when solving given problems is enhanced by better place value understanding (Reys, 2014).

References

A Learning Place. (n.d.). PLACE VALUE (kindergarten / Prep / Reception to Year 6) Teaching Resources Archives. Retrieved from https://alearningplace.com.au/category/teaching/teach-by-concept-teach/teach-number-algebra/teach-place-value/

Extranet Education. (n.d.). Number Expanders. Retrieved from https://extranet.education.unimelb.edu.au/SME/TNMY/Decimals/Decimals/teaching/models/nexpand.htm

Math Songs by NUMBEROCK. (2016, December 12). Place Value Song For Kids | Ones, Tens, and Hundreds | 1st Grade, 2nd Grade, 3rd Grade [Video file]. Retrieved from https://youtu.be/a4FXl4zb3E4

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy2.acu.edu.au

What were the big ideas?

This week the big ideas involved looking at Early Algebra also known a “Pre Algebra” and how the resources selected are linked with the skills and strategies involved. Similar to last week this week I learnt that the pre number concepts from week 6 are linked to the content this week, this is because skills such as patterning are also the key to starting to learn algebra. The connection between the concept of Algebra and patterning is the statement of a relationship.

Other big Ideas this week involved how number theory is linked to performing various strategies, as well as solving different levels of symbolic equations and expressions depending what level the student is at (Jamieson-Proctor, 2019). When students are able to make the progression to solving algebraic equations, they first need an understanding of the weeks 1-4 opperations addition, subtraction, multiplication and division as these are skills that are heavily connected to solving the symbolic equations.

My understanding of this weeks topic has changed, due to the fact I have learnt that surprisingly students in foundation year of school and early childhood centres actually engage in a variety of pre-algebra skills and concepts without even knowing it. Because of this in the future I can confidently introduce these concepts and explain their relationships while relating them back to the language model.

Algebra: one concept, skill or strategy

The skill of algebra is to determine what element is missing, when first learnkng this process it should start at the children’s language stage. However, it is recommended that a student should have a sufficient understanding of pre-number concepts (week 6). If a student is able to demonstrate this, then they should be able to perform the skill of algebra starting at the first level of the language model.

Algebra is built from the pre-number knowledge of patterning. Because of this student should already be able to use materials that they are familiar to recognise, describe, create, repeat, grow, replace and translate patterns. If a student can successfully demonstrate this then this would be the time where they transition to the materials language stage, which is simply using different materials to continue performing this same skill.

After this process, once a student reaches the mathematical stage of the language model they should then be introduced to the mathematical language of algebra. This is where they explore the meaning of words such as equations, equality and variables to help develop meaning. During this time would also be when the student is introduced to the related algebratic symbols also, but might still require the use of mathematical materials to help them further develop their ability to perform the skill of patterning.

Only once a student has reached the symbolic language stage of this model will they no longer need the asisstance of materials to help them perform these equations.

Misconceptions

Often a common misconception that students may develop with algebra is believe the equal sign determines or leads to the “answer,” when it is actually used as a sign of balance.

This can easily occur in younger students as many students are taught during earlier operations that number sentences always go “4 add 5 EQUALS 9 or 4 + 5 = 9.”  Instead of this students should be instructed that the numbers 4 and 5 even when placed on the right side of the equal sign will still give the same result as 9 because they are still EQUAL.

Therefore, to eliminate this misconception I would help students visualise the equal symbol as a sign of balance instead of a sign of ‘finding the answer.’ In order to achieve this, as a teacher I would have start using familiar materials just like the language model to physically model this concept, an example of this would be using a set of scales to demonstrate how the weight of each side needs to remain to achieve equality or balance. Following on from this, I would relate it back to an equation, stating that each side of this equal sign needs to be balanced in order to remain “Equal”.

 ACARA

Algebra, as also previously mentioned is first introduced within the foundation year, for students within the Australian Curriculum, Assessment and Reporting Authority (ACARA, 2019).

Mathematics/ Foundation Year/ Number and Algebra/ Patterns and algebra/ ACMNA005

Scootle Resource

Tessellate Decorate: Rectangles is one of the many Scootle resource that follows the ACARA code of ACMNA005, as this particular online resources aims to help students Demonstrate the properties of tessellations by providing models of different with the same rectangular shape. (Education Services Australia, 2013). This resource is aimed at children in the foundation year to year 2 in particular, as it successfully introduces early algebra skills of patterning and duplication. In this game students are required to decorate a room in a house with patterns made of rectangles, by selecting a tessellation of rectangles to make. Copy the given pattern and watch as it covers a part of the room (Education Services Australia, 2013).

This resource would be introduced to younger students when they are at the Children’s or Materials language stage of the Algebra language model, as children are using and understanding the more basic language of repeating and growing patterns. The limitations of this resource are the fact that it only provides visual patterns with no sound patterns, and there is only one shape focused on in this game. Because of this students who quickly progress may lose interest and may require a harder pattern problem to solve.

Al screenshots for this resource were retrieved from http://www.scootle.edu.au/ec/viewing/L7781/index.html

Resources or teaching strategies

Similar to typical domino cards, these cards display algebraic equations on one side and another equations answer on the other (Algebra Domino Loop Cards, n.d.). This particuar resource could either be used for student’s to rotate and play in small groups, as they could work together collaboratively to finish the domino line and work out the equations, or take it in turns individually to finish. This resource would mostly be utilised when students are at demonstrating things such as quick thinking strategies to solve the equation that aline with the symbolic language stage. These cards in the picture below would only be used for students with a high ability in algebra for example upper primary classes .

However, to make this tool more effective teachers could design and implement their own version of these domino cards and alter the level of ability by using easier or harder equations. Even by simply putting images on them would make this resource appropriate for struggling students at the materials language stage of the model. This resource proves to be very versatile and easy to implement in future classrooms.

Textbook: concept, skill or strategy

Reys chaper 15 part 1 displays the importance of developing an understanding of “the nature and prevalence of patterns in the world is an important part of teaching mathematics to primary school students” (Reys, 2014).

In studying this chapter I have learnt how traditionally, students do not begin to study algebra until they have a solid foundation in basic mathematial operations such as addition, subtraction, multiplication and division. However because of this, many students who have struggled in the past with maths never have the opportunity to properly learn algebra.

Problems, patterns and relations are all each proven to bean essential part of primary school mathematics. Therefore, the teaching of algebra in primary school should highlight this and focus more on ideas that are an essential part of the curriculum (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11751&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Algebra Domino Loop Cards. (n.d.). Retrieved from Twinkl:http://www.twinkl.co.uk/resource/t-n-1464-algebra-domino-loop-cards

Education Services Australia. (2013). Tessellate decorate: rectangles. Retrieved from http://www.scootle.edu.au/ec/viewing/L7781/index.html

Education Services Australia. (2019). Scootle resources. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA005

Jamieson-Proctor, R. (2018). EDMA241/262 Mathematics Learning and Teaching 1: Week 7 Part 3 (slide 5) Brisbane, Australia: Australian Catholic University. 

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au

What were the big ideas?

The Big Ideas in week 7 involved taking a closer look at Place Value and how we can use various resources in the classroom to demonstrate the relationships between this and other operations. Before this weeks lessons commenced I had a sound understanding of place value but only considered it to be mainly just the use of MAB blocks which has proven to be quite limiting. There were many connections made between the place value concept and the thinking strategies related to recalling multiplication facts.

As well as the many thinking strategies that help student to name, write, read, process and comprehend numbers in place value the value of a number depends on where it is placed in order for it to change (Jamieson-Proctor, 2019). During this week there were also clear links between the last weeks pre-number concepts and place value as it involves the understanding of the 3 main types of number and counting principles.

My conceptual understanding of this weeks topic has changed because I have learnt how students need to be able to comprehend numbers, and have a visual image mentally of what the number amount looks like before they can start learning how to say, write, and regroup it.

Because I now understand how large the concept of place value is and that it involves various skills and other conceptual understandings that become a prerequisite before a child can begin to learn it. Just like in the concept of division, a further emphasis need to be communicated to students about the value a number holds when it is placed in a numeral sentence, even if the number is zero.

Number & Place Value: one concept, skill or strategy

The main concept surrounding place value is that it is multiplicative. Initially this term may be difficult for students to comprehend, to develop a better understanding of this first students must be able to understand the concepts surrounding multiplication in order to rearrange numbers into certain positions to represent certain given values (Jamieson-Proctor, 2019).

When students first start learning this concept, they need to be introduced at the children’s language stage like any other foreign concept. This will enable them to build a solid picture in their head of what these numbers represent. By asking questions such as, “What does 15 look like?” children at this stage shouls be able to group materials like 20 toy cars or lollies togethe. With practice children can then move on to larger numbers like 120 that contain 3 digits in order to have a physical representation of what that number represents. By further using the method of regrouping those groups of twenty lollies into 6 groups of 20 or 12 groups of 10, students will be able to phyically see that the value of 120 is is way bigger than the value of 20.

Misconceptions

As previously mentioned place value is a key concept for children to get to grasp, without an understanding of it they will struggle to the 4 main operations, let alone read and write basic numbers. Building on from early counting and pre-number concepts place value is basically the recognition of cardinal numbers to knowing the value of each digit in a number. In schools this is usually done to develop an understanding of our base-10 structure which is frequently use in everyday life for things such as currency.

A common misconception surrounding the place value concept is the need for stuents to “recognize 0 as a label for an empty set, or nothing, as well as a place holder for numbers in our base-10 structure” (Broadbent Math, 2015) to avoid confusion. It becomes more of an obvious issue when multiplying by 10 or 100, with zeroes magically ‘added’ to a number. This needs to be broken down and modelled with 2-digit numbers and multiple physical and visual representations so they can see the effect on each digit when numbers are 10 or 100 times bigger right infront of them with familliar materials.

ACARA

The concept of Place Value is first introduced within the foundation year, for students within the Australian Curriculum, Assessment and Reporting Authority (ACARA, 2019). This is mainly because the place value concept involves understanding the value of a number, in order to be able to do this students must first have a solid understanding of pre-number concepts.

Mathematics/ Foundation Year/ Number and Algebra/ Number and place value/ ACMNA002

Scootle Resource

Wishball Challenge: Tens is a Scootle resource that works as an interactive place value chart. This particular resource is designed for students in year level 2, as students are required to challenge their understanding of place value in whole numbers up to 99. At the start of this game students receive a starting number, such as 86, and work towards turning it into a target number, such as 24, within the limit 20 turns.The overall purpose if this online activity is to try to achieve the target in as few turns as possible (Education Services Australia, 2016).

It would be smart to utilise this resource when students are at the mathematical stage of the language model, where students already understand the concept of place value, and are applying the skill of representing numbers up to 99.

Compared to similar resources, this resource cleverly displays numbers in various forms to make it easier for students to picture the outcome exapmples of this as shown above incoude a number line format, the number itself in symbolic form and a place value chart. This particular resource is 1 out of three that focus on different levels Wishball Challenge: Hundreds and Wishball Challenge: Thousands are two other versions designed for students that are ready to progress to using bigger units .

Resources or teaching strategies

This Place Value Abacus video is an easily accessible teaching resource used to demonstrate place value and help students gain a visual understanding of place holding within this system.

This video breaks down place value perfcctly and could be used  for children from years 1 if dealing with smaller units or 2 upwards, mainly when students reach the mathematical stage of the language model. This would mainly be because they have not fully understood the concept of place value and require visual aids, and they are using the mathematical language of thousands, hundreds, tens, ones etc throughout the entireity of the video. This resource could be further developed and utilised in classroom to also show representations of decimals and the place value system of more complex places like tenths, hundredths etc to increase difficulty. Overall, the explanations throughout the video are simple enough to follow and replicate, while being effective for children to use individually to understand the skill of writing numbers in the correct place.

Textbook reading: one concept, skill or strategy

As discussed in the previous chapter, Reys starts chapter 8 with a recap stating “early number sense and counting naturally leads to place value as an organisational structure for number” (Reys, 2014). Backing up this statement he continues by explaining that the same principles for smaller numbers are involved as larger numbers are counted also. Representations no matter the type for larger numbers are still based on learning the pattern or sequence in a meaningful way to make concrete connections. Place value remains an important transition between symbols and language making it important to correctly model for students to avoid further misconceptions. Place value throughout all of students work links whole numbers, the 4 operations, the metric system and decimals (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11751&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Broadbent Maths. (2015). Place value – representation and misconceptions. Retrieved from https://www.broadbentmaths.com/pages/place_value__representation_and_misconceptions_255363.cfm

Education Services Australia. (2016). Wishball challenge: tens. Retrieved from http://www.scootle.edu.au/ec/viewing/L8459/L8459/index.html#

Jamieson-Proctor, R. (2019). EDMA241/262 Mathematics Learning and Teaching 1: Week 6 Part 2 (slide 3-7) Brisbane, Australia: Australian Catholic University. 

Matholia. (2013, June 26). Place Value – Abacus [Video file]. Retrieved from https://youtu.be/QcpW-N_zHWk

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au

Scootle. (2019). Home. Retrieved from https://www.scootle.edu.au/ec/p/home

What were the big ideas?

The big ideas included in the lecutre of week 6 involved looking at pre-number concepts. After this week I now understand how patterning connects all of these pre-number concepts together. During this week it was also discussed how pre-number principles are prerequisite skills for being able to perform all the stages of the counting principles to an adequate standard. Because of these discussions I am now able to visualise the relationships between all three types of numbers and the counting principles, as some things can be counted and others cannot-therefore students need to understand when to apply this recent knowledge.

My understanding of this weekly topic has definitely changed as I have learnt the importance of students being able to develop pictures in their heads to recognise patterns immediately. In the future during lessons I will be able to recognise if students can understand all five counting principles, and if they are struggling to grasp these concepts how I can adjust their learning by using the other big ideas.

Multiplication: One concept, skill or strategy

The concept of patterning links all the pre-number mathematics concepts together, as it requires skills such as determining, matching, sorting, comparing and ordering. patterning is the repeating of sets, these representations can vary from visual, auditory or through patterns that incorporate movement. Patterning encourages children to use all of their senses to organise and remember mathematical ideas and relationships making it an important concept to learn early. Using patterns in the classroom can be a fun and engaging way to teach problem solving. To completely understand the concept of patterning successfully, children must demonstrate these various skills:

• Construct patterns
• Directly Copy patterns
• Create their own personal patterns
• Extend already exsisting patterns

Overall, as a pre-number concept children are exposed to patterning very young, and can pick up patterns before they are even taught the concept at school. In oder for a student to do well in later mathematics such as algebra and geometry they must understanding the importance of patterning as a prerequisite.

Misconceptions

A common misconception that children may develop when learning to perform the skill of patterning if taught incorrectly is when they see a pattern and don’t understand that patterns are repeating ‘sets’.

Patterning is very important because it requires a skill to organise and remember relationships. If a student does struggle to recognise patterning as repeated sets, they may miss and become unable to visualise the relationship between the sets as they keep repeating. Something that could affect this is if the student cannot perform determining, matching, sorting, comparing or ordering skills from the earlier pre-number concepts. If a child must first recognise the sets of patterns they are give or they will not be able to build upon it , extend it or insert missing links.

In the future to avoid this misconception I would allow more time for the students to revise their skills to make sure they can all determine, match, sort, compare and order to a satisfactory level. To complete this I would use familliar materials and vocabulary associated with the the children’s language stage, For example words such as ‘describe’ and ‘match’. Only when students can perform these tasks will I re-introduce patterning followed by an explanation about how patterns are sets. Using demonstrations with coloured blocks would also enhance the explanation and allowing student to visualise the relationships.

ACARA

Sorting is first introduced to students in the Foundation year within The Australian Curriculum Assessment and Reporting Authority (ACARA, 2017). However, technically it was first introduced during the early childhood education years (0-5) because sorting is considered a natural skill that children instincively develop.

Mathematics/Foundation Year/ Number and Algebra/ Patterns and algebra/ ACMNA005

Scootle Resource

Monster Choir: Making Patterns is a Scootle resource that is recommended for children from the Foundation year into grade 2. Students are simply required to help a group of monsters in a choir to make specific animal sounds in order. Students are able to make a sequence of up to four sounds. By choosing the correct monsters will mean their sounds match the sequence. Repeating the pattern will make a song (Education Service Australia, 2016).

This game is a good resource and would be used when children are at the mathematical language stage because it uses language like “match” and doesn’t include symbols. Students who are in the foundation year would find this enjoyable, but may become difficult if they are unable read, as the game only uses voice commands and instructions at the very start of the game. However, the game is easy to figure out and also allows children who find it easy to test themselves and adjust the difficulty level. Overall this is a good example of a resource that will successfully encourage sorting and matching skills.

Resources or Teaching strategies

This particular resource is an online game that helps children learn patterning on their computer. Children in the foundation year of school could easily use this when practicing the skill of patterning. All the student has to do is insert the missing shape into the pattern correctly or add what shape would be next in that set.

Children would most likely use a resource ike this when they are at the materials language stage as they have to extend or complete the given patterns using various colours and shapes that they recognise. Unlike other various sources similar to this, the game is not limited to a small number of patterns to complete. If students find this too easy or advanced, they have the ability tomove to a higher or lower level to suit their ability.

Textbook: concept,skill or strategy

Reys Chapter 7 part 1 discusses the different types of early number situations that young children are exposed to (As shown in the concept map above). Reys desribes early number concepts as the foundation of for building later skills involving numbers. It is important that Early childhood educators help children take advantage of their intuitive mathematical learning. There are different steps that are involved when trying to develop prenumber concepts compared to regular conpets later on that can eventually lead to meaningful counting skills and number sense at a fluent level (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11751&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2016). Monster Choir: making patterns. Retrieved from http://www.scootle.edu.au/ec/viewing/L1056/index.html

Jamieson-Proctor, R. (2019). EDMA241/262 Mathematics Learning and Teaching 1: Week 5 Part 1 (slide 6-24) and Brisbane, Australia: Australian Catholic University.

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au

Topmarks. (2019). Shape, Position and Movement, Maths Games. Retrieved from https://www.topmarks.co.uk/maths-games/3-5-years/shape-position-and-movement

What were the big ideas?

When starting to learn the concept of division students should already have a sound understanding of the previous skills and strategies for the concept of multiplication. This is beacuse just like addition and subtraction, there is an inverse relationship between the two.

The concept of division is to separate any number into equal parts that are smaller. This process of seperation can be shown in two different ways: Partition and Quotition. Partition, which is also frequently referred to as sharing, is when a number is divided into multiple groups to see how many of something each group will get. Quotition however, is also known as repeated subtraction, where a small quantity is repeatedly subtracted from a larger amount in order to find the number of groups needed to divide the total. With multiplication, we know the number of groups and the size of each group. The total is unknown. However, with division we know the total amount, but need to determine either the number of groups or the size of each group (ORIGO Education & DePaul, 2017).

My understanding of the weekly topic has changed. I am now able to clearly see how the previous four operations are all linked together. Because of these new understandings as a teacher in the future, I will make sure that I give my students a good concrete foundation for learning the concepts by modellnig them in different ways before moving onto the next. I will also provide them with the appropriate skills, strategies and terminology to solve these problems, no matter how they are displayed.

Division: One concept, skill or strategy

A popular strategy of division is the Think Multiplication strategy. This is a strategy that requires students to revisit their prior knowledge of multiplication, and use that knowledge to solve division problems because they are inverse operations. Being able to understand this will help students develop a better level of proficiency and fluency equally in both operations.

An example of this strategy is when faced with the problem stating 40 divided by 4, students can use this think multiplication strategy to recall their multiplication facts of 4. Remembering that when 4 is multiplied by 10 it equals 40, therefore 40 is divided by 4 must it equal 10. Understanding this opposite relationship is important to solving these problems.

Misconceptions

A common misconception related to the concept of division is becoming confused when dividing by the number ‘0’. The concept of this number, or ‘nothing’ in our symbolic language can cause a large amount of difficulty for early learners of mathematics. It is well known that dividing by 0 cannot physically be done.For example when students are presented with a problem such as, ‘I have 8 chocolates, but 0 friends, how many chocolates can I give to my 0 friends’. Students may not be able to mentally visualise this or be able to model their ideas in a picture or diagram.

To eliminate this particular misconception I would make sure that the students understand what it means to be displayed with the representation of “0” and how they can easily approach problems similar to this. By working through the multiple language model stages, I will be able to use familiar materials and vocabulary to assist students in developing a concrete understanding of the concept of dividing by ‘0’.

ACARA

Division is first introduced to students in grade 2 for students within Australian Curriculum Assessment and Reporting Authority (ACARA, 2019).

Mathematics/ Year 2/ Number and Algebra/ Number and place value/ ACMNA032

Scootle Resource

The Divider is a Scootle resource that can be utilised in classrooms for students in year 2, 3 and 4. Students are required to break down larger division problems into smaller, more manageable sized pieces. In this task students are required to solve a division problem by breaking it doen into two halves and only solving it up to the larger part they know. This is demonstrating the Quotition method as the final answer is how many times the smaller number can be taken away from the larger and is not trying to equally distribute any products.

 This resource would be appropriate to use at the symbolic language stage of the language model as it purely uses the division symbol to represent what needs to be done in this equation and doesn’t include words such as ‘share’. By breaking down the problems it also allows students to show the fact families and utilise the previously discussed think multiplication strategy.

Resources or Teaching strategies

This children’s picture book Divide and Ride by Stuart Murphy and George Ulrich, is a great teachers resource to use when introducing students to the concept of division. The story follows eleven friends at a carnival that have to divide themselves up into different groups to ride the many carnival rides at the themepark (for example: a 2-per-seat roller coaster and a 4-per-cup teacup ride). Just like all of the other MathStart books,at the end there’s a section that includes helpful tips for teaching division lessons (the best children’s books, 2019).

Textbook: concept,skill or strategy

Throughout chapter 11 section 5 Reys relates all mathematical algorithims and strategies back to the use of real world problems and explains why is the best approach for learning about division. Just like the language model Reys agrees that the most important thing is for students to develop an initial understanding of what division is all about is to utilise concrete materials to model division situations just like other operations and to help explain their thinking. A teacher can scaffold students to record their thinking clearly and efficiently on paper. But in order for it to have meaning it needs to be carefully connected to the concrete experience of division (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11753&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2013). The divider: without remainders. Retrieved from http://www.scootle.edu.au/ec/viewing/L2007/index.html

ORIGO Education, & DePaul, D. (2019). Teaching Division Facts: Why the Think-Multiplication Strategy Works. Retrieved from https://www.origoeducation.com/blog/think-multiplication-strategy/

Scootle. (2019). Home. Retrieved from http://www.scootle.edu.au/ec/p/home

The Best Children’s Books. (2019). The Best Children’s Books! — Teachers’ Picks. Retrieved from https://www.the-best-childrens-books.org

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy2.acu.edu.au

What were the big ideas?

the big ideas included in week 4 involved exploring the concept of multiplication and the relationship between that and addition, becuase it is simply described as repeated addition of equal groups. Due to this being the case, students must have a strong understanding of the concept of addition before being introduced to the multiplication concept.

There are various ways we can visually model multiplication problems to assist students in grasping the concept of multiplication. The main 4 commonly used in classroom or frequently referred to are set, array, measurement and combinations each one has a different physical representation of the multiplication concept. Visually representing these models has become an important teaching tool in getting students to see these relationships.

Multiplication: One concept, skill or strategy

When working with the facts that have even numbers such as2, 4 and8 as one of the factors, you can use the Doubles Strategy. Using proportional adjustment to solve multiplication problems such as doubling, can be used to make larger multiplication problems easier to solve. For example, 3 x 16 is the same as 6 x 8. By utilising this strategy, it also allows students to realise commutative laws such as 6 x 8 and 8 x 6 being the same and achieving the same answer, making it easier to retain multiplication facts mentally. 

Misconceptions

A common misconception about multiplication is that frequently most students do not understand the commutative or turnaround properties of the multiplication facts they are supposed to mentally retain. The reason this particular misconception might occur is because multiplication problems are represented in different ways, such as 6 x 10, or 6 groups of 10, being the same as 10 x 6, or 10 groups of 6 which may easily confuse children . Students may not be able to understand the commutative or ‘turnaround’ property that is associated with multiplication, meaning the order in which the factors are written does not make a difference to finding the right answer or “Product”. 

By being equipped with different strategies to make solving multiplication problems more efficient we can stop students from being overwhelmed by having to remember so many multiplication facts.

Because of this in the future to prevent this misconception from occurring by demonstrating as soon as possible the ‘turnaround’ principle within multiplication, where 10 x 6 and 6 x 10 are equal. I will also make sure that I use the correct language and terminology when doing this, such as ‘turnaround’, while utilising array models to represent this visually, so that students can visualise this when faced with a similar problem.

ACARA

Multiplication is first introduced within the Australian Curriculum in Year 2, for students within the (ACARA, v8.3, 2017).

Mathematics/ Year 2/ Number and Algebra/ Number and place value/ ACMNA013

Scootle Resource

The aim of this interactive game is to help creatures line up and walk through gates. But in order for them to be able to move through the gates the rows and columns must be equal. For example, start with 23 pobbles. Students must make a prediction to whether the number can be divided into an equal number of rows. If not, they can then add or subtract pobbles to make a number that will work for them to move through the gates.

Students are introduced to the commutative property of multiplication. A dynamic array provides a visual model to support understanding of the multiplicative relationship between factors.

Education Services Australia, 2013

Resources or Teaching strategies

This array’s worksheet is a resource that could be used to demonstrate the concept of multiplication. Students are required to fill in the blanks on this sheet in various ways such as a visual array and symbolic math scentence. It shows the students the many ways that they can represent multiplication, in order to gain more of a concrete understanding of the concept due to the assisstance of pictures.

This resource would be appropriate to use at the beginning of the symbolic stage of the language model, as students represent their answers using worded problems in conjunction with symbols and number sentences. However, this resource has limitations as some students who struggle to grasp the concept need physical objects such as counters and blocks to touch and move in order to visually represent and conceptualise multiplication.

Textbook : concept,skill or strategy

In chapter 11 part 4 Reys explains the importance of students having a well developed and deep understanding of prerequisites to multiplication such as place value, expanded notation, addition methods and the distributive property, along with the knowledge of basic multiplication facts. He also revises the use of certain Mathematical language associated with any method and how this need to be encouraged. This will allow the teacher to have more of an insight into how their student’s think (Reys, 2014).

References

ACARA. (2019). Mathematics. Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11753&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2013). Pobble arrays: make multiples. Retrieved from http://www.scootle.edu.au/ec/viewing/L2056/index.html

Education Services Australia. (2019). Multiplication Resources. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA031

Mathematics Shed. (2018). Multiplication Resources. Retrieved from http://www.mathematicshed.com/multiplication-resources-shed.html

ORIGO Education, & DePaul, D. (2019). The Doubling Strategy for Multiplication. Retrieved from https://www.origoeducation.com/blog/doubling-strategy-for-multiplication/

Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au

 What were the big ideas?

When looking at subtraction, students should have a sound understanding of the concepts, skills and strategies for addition, as there is an inverse relationship between the two, and one is a pre-requisite for the other. That is why addition is taught first, before introducing the concept of subtraction (Jamieson-Proctor, 2019).

My understanding of the weekly topic has definitely changed as I myself learnt the importance of the relationship between Subtraction and Addition. I should remember that these are two different things, that correspond to each other.

Therefore, these new understandings will shape my future teaching as I will know the difference between the two concepts, and be mindful of using the correct terminology and language. I will also make sure that my students have a strong understanding of the concept of addition before introducing them to the concept of subtraction.

Subtraction: concept, skill or strategy

A skill of subtraction concept  is decomposition, which is a subtraction algorithm. This is a useful skill as it helps students to subtract one number from another number, by trading larger amounts to break up or “decompose” the parts into smaller more manageable parts. However, in order to be able to grasp this skills students must first understand subtraction concept, as well as place value.

By using physical materials such as MAB blocks, it allows the students to build larger numbers and model essential operations and skills, a place value mat with counters may be an appropriate method also. Students are required to know that they only build the total when subtracting, for example when subtracting 22 from 50, we build 50, as it is that number is total.

Misconceptions

A common misconception many students have about subtraction is that there is only one type of subtraction, and that is ‘take-away’. There are three different types of situations when dealing with subtraction equations. The firstone students are most likely to learn early on in school and the easiest, is called “separation” or most commonly known as taking away. This is where one amount is taken away from another to find out the total that is left. The second is comparison, in which two amounts are compared against each other to find the difference. The third is part-whole, where the amount in the whole set and one part are already known or given, and may be used to find out how many are in the unknown part.

Early instruction relating to subtraction for younger students should provide various opportunities for children to explore these different types of subtraction situations. Children learn the meaning of subtraction through physical concrete experiences in the classroom and then learn to record these equations in different forms. Using manipulatives such as counters or other objects to model subtraction situations is extremely important to develop childrens understandings as well as gain interest.

By drawing pictures and using illustrations, children can make the transition to a more symbolic understanding of subtraction. These visual models help children make the connection between the actual items and the numbers and operational symbols used to represent them in a subtraction sentence.

As a students math ability progresses through school, they will continue to use physical manipulatives and pictures to model larger subtraction situations as well as the inverse relationship between addition and subtraction. By drawing these pictures and using illustrations at a younger age, students can make this transition to a more symbolic understanding of subtraction much easier (Houghton Mifflin Math, 2006).

ACARA

Subtraction is first introduced within the Australian Curriculum in Year 1 for students within the Australian Curriculum, Assessment and Reporting Authority (ACARA, 2019).

Mathematics/ Year 1/ Number and Algebra/ Number and place value/ ACMNA015

Scootle Resource

Counting beetles: making word problems is a Scootle resource that can be used for children from the foundation year, grade 1 and grade 2. Students firstly are required to choose whether they would like to add or subtract. They are then required to select the number of beetles for their problem, and are asked to use the number line to show how to solve the problem. Then the students are required to make a number sentence to match the number line. This activity provides opportunities for students to explore and construc,t number lines, and how useful it is to solve addition and subtraction problems. It also promotes the connection between worded problems, number line models and simple equations.

This resource could be used to demonstrate the skill of using a number line to add groups together. It shows the process of counting on when moving up the number line, and allows students to efficiently and effectively obtain an answer. This resource would be appropriate to use at the mathematical language stage, moving towards the symbolic language stage. It uses a combination of graphics, word problems such as ‘ 3 more beetles came’, diagrams such as the number line, and symbolic representations such as ‘5+3=8’. This resource could be more beneficial for students if it asked the students to reverse the order of the worded problem, the number line and the number sentence. This would perhaps allow for further understanding and comprehension of how these representations are all linked.

Resources or Teaching Strategies

A Strategy Sheet is a resource designed to demonstrate the concept of subtraction. Students are required to read the given word problem at the top of the page and display it using different strategies such as the use of materials, pictures, and a number sentence at the bottom. It shows students the various ways of representing subtraction, in order to gain a more concrete understanding of the concept. This particular resource would be appropriate to use at the very beginning of the symbolic stage of the language model, as students introduced to symbols and number sentences as a way of expressing their ideas. However, this worksheet could be better if the middle was blank so students who have demonstrated a better understanding of the concept could design their own word problems.

Textbook: Concept, skill or strategy

During chapter 11 section 3 Reys explores the standard subtraction algorithm known as decomposition using MAB blocks to form a conceptual understanding of subtraction in a more physical way. This strategy is a very important tool for students to develop the trading and grouping skills that are used when doing subtraction equations. This particular strategy can be first introduced/ is more suitable for students in year 2 within the Australian Curriculum (Number and Algebra: Students solve simple addition and subtraction problems using a range of efficient mental and written strategies ACMNA030). This strategy can be easily altered to demonstrate more difficult problems including hundreds or thousands MAB’s to extend the students skills and knowledge in this operation.

References

ACARA. (2019). Curriculum: Year 1, Mathematics, Number and Algebra, Number and place value (ACMNA015). Retrieved from https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11752&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Statistics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability=Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking&capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability=Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander+Histories+and+Cultures&priority=Asia+and+Australia’s+Engagement+with+Asia&priority=Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false

Education Services Australia. (2011). counting beetles. Retrieved from http://www.scootle.edu.au/ec/viewing/L8284/index.html

Houghton Mifflin Math. (2006). Modeling Subtraction: Overview. Retrieved from https://www.eduplace.com/math/mw/background/1/02/te_1_02_overview.html

Jamieson-Proctor, R. (2019). EDMA241/262 Mathematics Learning and Teaching 1:                     Week 3. Online lecture, Australian Catholic University.

Reys, Robert E.. HELPING CHILDREN LEARN MATHEMATICS 2E, Wiley, 2014. ProQuest Ebook Central, https://ebookcentral-proquest-com.ezproxy2.acu.edu.au/lib/acu/detail.action?docID=4748099.

Scootle. (2019). Scootle Resources. Retrieved from https://www.scootle.edu.au/ec/viewMetadata.action?id=L8284&q=subtraction&topic=&start=0&sort=relevance&contentsource=&contentprovider=&resourcetype=&v=text&showBookmarkedResources=&showLomCommercialResources=false&field=title&field=text.all&field=topic&learningarea=all&contenttype=%22Interactive%20resource%22&contenttype=%22Teacher%20guide%22&commResContentType=all&commResContentType=%22App%20(mobile)%22&commResContentType=%22Audio%22&commResContentType=%22Book%20(electronic)%22&commResContentType=%22Book%20(printed)%22&commResContentType=%22Digital%20item%22&commResContentType=%22Learning%20object%22&commResContentType=%22Other%22&commResContentType=%22Printed%20item%22&commResContentType=%22Software%22&commResContentType=%22Teacher%20resource%22&commResContentType=%22Video%22&userlevel=(0%20OR%201%20OR%202)&kc=any&lom=true&scot=true&follow=true&topiccounts=true&rows=20&suggestedResources=M024882,S4970,M019626,M008812,M019410,M019628,L8280,S6184,M014006,R11490,M009191,M008811,R11395,M019622,M019624&fromSearch=true

Teachers Pay Teachers. (2019). Subtraction within 10 Word Problems Worksheets. Retrieved from https://www.teacherspayteachers.com/Product/Subtraction-within-10-Word-Problems-Worksheets-860475