What were the big ideas?
This week the big ideas involved looking at Early Algebra also known a “Pre Algebra” and how the resources selected are linked with the skills and strategies involved. Similar to last week this week I learnt that the pre number concepts from week 6 are linked to the content this week, this is because skills such as patterning are also the key to starting to learn algebra. The connection between the concept of Algebra and patterning is the statement of a relationship.
Other big Ideas this week involved how number theory is linked to performing various strategies, as well as solving different levels of symbolic equations and expressions depending what level the student is at (Jamieson-Proctor, 2019). When students are able to make the progression to solving algebraic equations, they first need an understanding of the weeks 1-4 opperations addition, subtraction, multiplication and division as these are skills that are heavily connected to solving the symbolic equations.
My understanding of this weeks topic has changed, due to the fact I have learnt that surprisingly students in foundation year of school and early childhood centres actually engage in a variety of pre-algebra skills and concepts without even knowing it. Because of this in the future I can confidently introduce these concepts and explain their relationships while relating them back to the language model.
Algebra: one concept, skill or strategy
The skill of algebra is to determine what element is missing, when first learnkng this process it should start at the children’s language stage. However, it is recommended that a student should have a sufficient understanding of pre-number concepts (week 6). If a student is able to demonstrate this, then they should be able to perform the skill of algebra starting at the first level of the language model.
Algebra is built from the pre-number knowledge of patterning. Because of this student should already be able to use materials that they are familiar to recognise, describe, create, repeat, grow, replace and translate patterns. If a student can successfully demonstrate this then this would be the time where they transition to the materials language stage, which is simply using different materials to continue performing this same skill.
After this process, once a student reaches the mathematical stage of the language model they should then be introduced to the mathematical language of algebra. This is where they explore the meaning of words such as equations, equality and variables to help develop meaning. During this time would also be when the student is introduced to the related algebratic symbols also, but might still require the use of mathematical materials to help them further develop their ability to perform the skill of patterning.
Only once a student has reached the symbolic language stage of this model will they no longer need the asisstance of materials to help them perform these equations.
Misconceptions
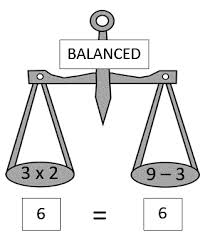
Often a common misconception that students may develop with algebra is believe the equal sign determines or leads to the “answer,” when it is actually used as a sign of balance.
This can easily occur in younger students as many students are taught during earlier operations that number sentences always go “4 add 5 EQUALS 9 or 4 + 5 = 9.” Instead of this students should be instructed that the numbers 4 and 5 even when placed on the right side of the equal sign will still give the same result as 9 because they are still EQUAL.
Therefore, to eliminate this misconception I would help students visualise the equal symbol as a sign of balance instead of a sign of ‘finding the answer.’ In order to achieve this, as a teacher I would have start using familiar materials just like the language model to physically model this concept, an example of this would be using a set of scales to demonstrate how the weight of each side needs to remain to achieve equality or balance. Following on from this, I would relate it back to an equation, stating that each side of this equal sign needs to be balanced in order to remain “Equal”.
ACARA
Algebra, as also previously mentioned is first introduced within the foundation year, for students within the Australian Curriculum, Assessment and Reporting Authority (ACARA, 2019).
Mathematics/ Foundation Year/ Number and Algebra/ Patterns and algebra/ ACMNA005

Scootle Resource
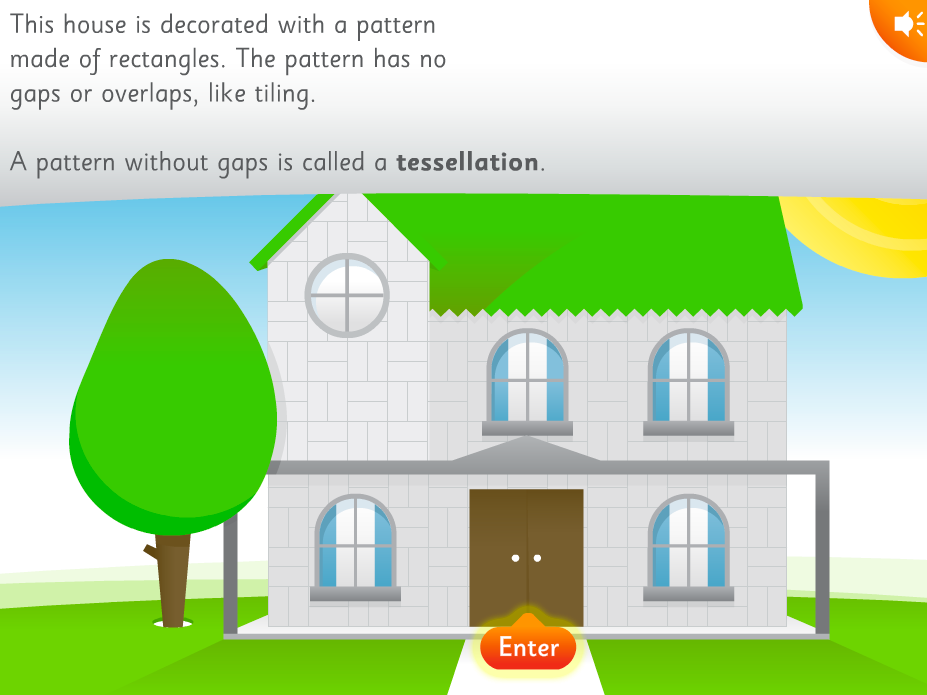
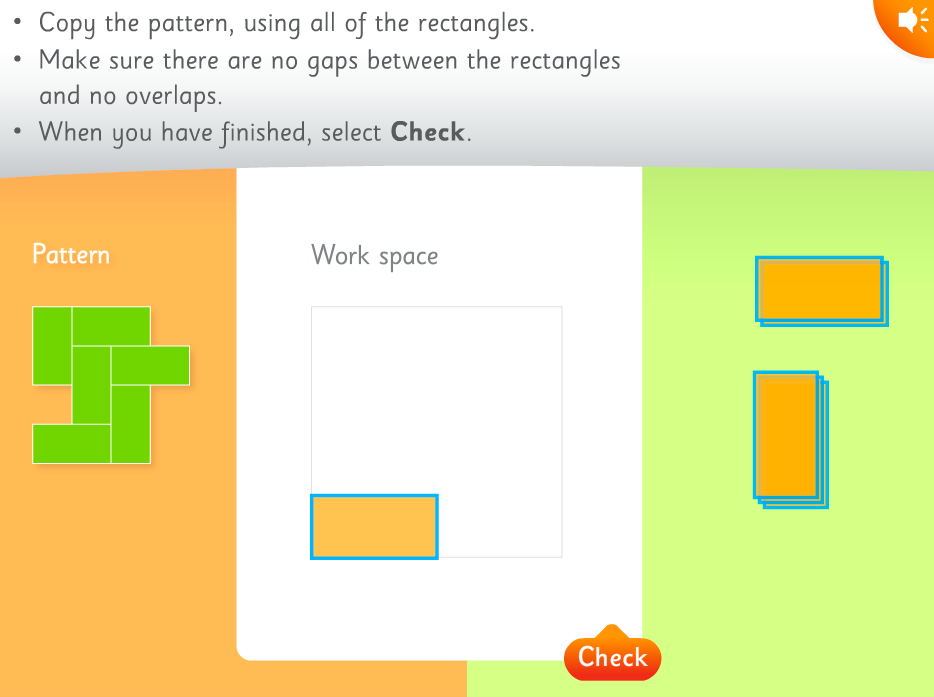
Tessellate Decorate: Rectangles is one of the many Scootle resource that follows the ACARA code of ACMNA005, as this particular online resources aims to help students Demonstrate the properties of tessellations by providing models of different with the same rectangular shape. (Education Services Australia, 2013). This resource is aimed at children in the foundation year to year 2 in particular, as it successfully introduces early algebra skills of patterning and duplication. In this game students are required to decorate a room in a house with patterns made of rectangles, by selecting a tessellation of rectangles to make. Copy the given pattern and watch as it covers a part of the room (Education Services Australia, 2013).
This resource would be introduced to younger students when they are at the Children’s or Materials language stage of the Algebra language model, as children are using and understanding the more basic language of repeating and growing patterns. The limitations of this resource are the fact that it only provides visual patterns with no sound patterns, and there is only one shape focused on in this game. Because of this students who quickly progress may lose interest and may require a harder pattern problem to solve.
Al screenshots for this resource were retrieved from http://www.scootle.edu.au/ec/viewing/L7781/index.html

Resources or teaching strategies
Similar to typical domino cards, these cards display algebraic equations on one side and another equations answer on the other (Algebra Domino Loop Cards, n.d.). This particuar resource could either be used for student’s to rotate and play in small groups, as they could work together collaboratively to finish the domino line and work out the equations, or take it in turns individually to finish. This resource would mostly be utilised when students are at demonstrating things such as quick thinking strategies to solve the equation that aline with the symbolic language stage. These cards in the picture below would only be used for students with a high ability in algebra for example upper primary classes .

However, to make this tool more effective teachers could design and implement their own version of these domino cards and alter the level of ability by using easier or harder equations. Even by simply putting images on them would make this resource appropriate for struggling students at the materials language stage of the model. This resource proves to be very versatile and easy to implement in future classrooms.
Textbook: concept, skill or strategy
Reys chaper 15 part 1 displays the importance of developing an understanding of “the nature and prevalence of patterns in the world is an important part of teaching mathematics to primary school students” (Reys, 2014).
In studying this chapter I have learnt how traditionally, students do not begin to study algebra until they have a solid foundation in basic mathematial operations such as addition, subtraction, multiplication and division. However because of this, many students who have struggled in the past with maths never have the opportunity to properly learn algebra.
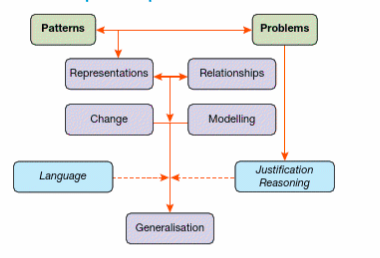
Problems, patterns and relations are all each proven to bean essential part of primary school mathematics. Therefore, the teaching of algebra in primary school should highlight this and focus more on ideas that are an essential part of the curriculum (Reys, 2014).
References
Algebra Domino Loop Cards. (n.d.). Retrieved from Twinkl:http://www.twinkl.co.uk/resource/t-n-1464-algebra-domino-loop-cards
Education Services Australia. (2013). Tessellate decorate: rectangles. Retrieved from http://www.scootle.edu.au/ec/viewing/L7781/index.html
Education Services Australia. (2019). Scootle resources. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA005
Jamieson-Proctor, R. (2018). EDMA241/262 Mathematics Learning and Teaching 1: Week 7 Part 3 (slide 5) Brisbane, Australia: Australian Catholic University.
Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au