What were the big ideas?
The Big Ideas in week 7 involved taking a closer look at Place Value and how we can use various resources in the classroom to demonstrate the relationships between this and other operations. Before this weeks lessons commenced I had a sound understanding of place value but only considered it to be mainly just the use of MAB blocks which has proven to be quite limiting. There were many connections made between the place value concept and the thinking strategies related to recalling multiplication facts.
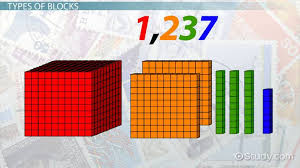
As well as the many thinking strategies that help student to name, write, read, process and comprehend numbers in place value the value of a number depends on where it is placed in order for it to change (Jamieson-Proctor, 2019). During this week there were also clear links between the last weeks pre-number concepts and place value as it involves the understanding of the 3 main types of number and counting principles.
My conceptual understanding of this weeks topic has changed because I have learnt how students need to be able to comprehend numbers, and have a visual image mentally of what the number amount looks like before they can start learning how to say, write, and regroup it.
Because I now understand how large the concept of place value is and that it involves various skills and other conceptual understandings that become a prerequisite before a child can begin to learn it. Just like in the concept of division, a further emphasis need to be communicated to students about the value a number holds when it is placed in a numeral sentence, even if the number is zero.
Number & Place Value: one concept, skill or strategy
The main concept surrounding place value is that it is multiplicative. Initially this term may be difficult for students to comprehend, to develop a better understanding of this first students must be able to understand the concepts surrounding multiplication in order to rearrange numbers into certain positions to represent certain given values (Jamieson-Proctor, 2019).
When students first start learning this concept, they need to be introduced at the children’s language stage like any other foreign concept. This will enable them to build a solid picture in their head of what these numbers represent. By asking questions such as, “What does 15 look like?” children at this stage shouls be able to group materials like 20 toy cars or lollies togethe. With practice children can then move on to larger numbers like 120 that contain 3 digits in order to have a physical representation of what that number represents. By further using the method of regrouping those groups of twenty lollies into 6 groups of 20 or 12 groups of 10, students will be able to phyically see that the value of 120 is is way bigger than the value of 20.
Misconceptions
As previously mentioned place value is a key concept for children to get to grasp, without an understanding of it they will struggle to the 4 main operations, let alone read and write basic numbers. Building on from early counting and pre-number concepts place value is basically the recognition of cardinal numbers to knowing the value of each digit in a number. In schools this is usually done to develop an understanding of our base-10 structure which is frequently use in everyday life for things such as currency.
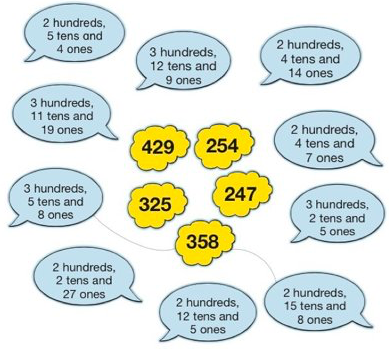
A common misconception surrounding the place value concept is the need for stuents to “recognize 0 as a label for an empty set, or nothing, as well as a place holder for numbers in our base-10 structure” (Broadbent Math, 2015) to avoid confusion. It becomes more of an obvious issue when multiplying by 10 or 100, with zeroes magically ‘added’ to a number. This needs to be broken down and modelled with 2-digit numbers and multiple physical and visual representations so they can see the effect on each digit when numbers are 10 or 100 times bigger right infront of them with familliar materials.
ACARA
The concept of Place Value is first introduced within the foundation year, for students within the Australian Curriculum, Assessment and Reporting Authority (ACARA, 2019). This is mainly because the place value concept involves understanding the value of a number, in order to be able to do this students must first have a solid understanding of pre-number concepts.
Mathematics/ Foundation Year/ Number and Algebra/ Number and place value/ ACMNA002

Scootle Resource
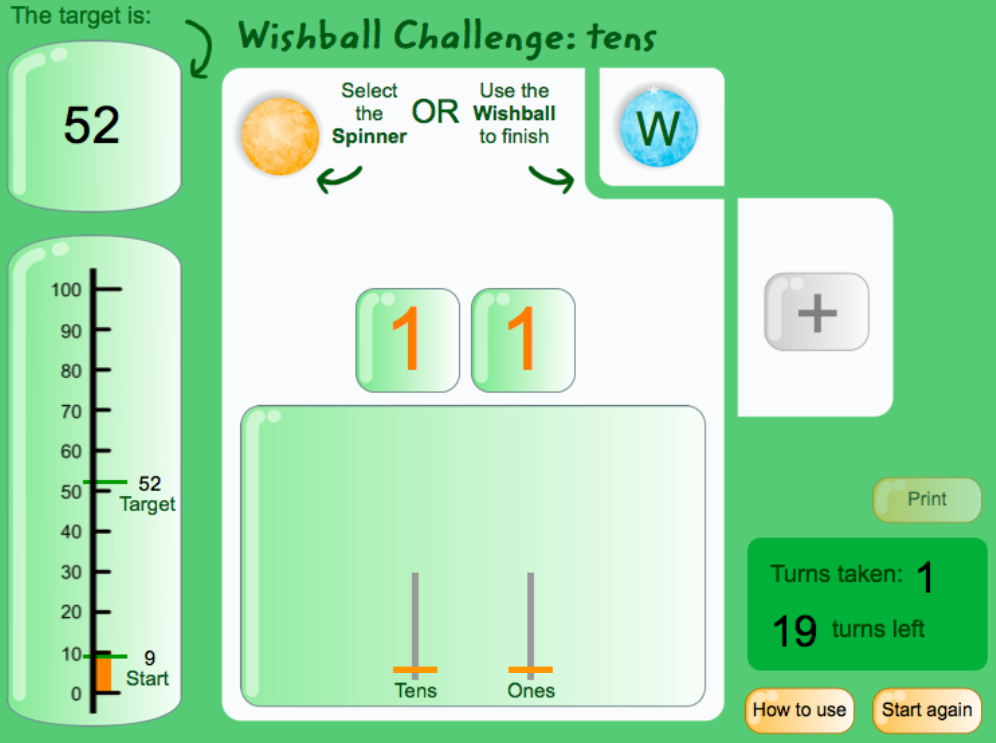
Wishball Challenge: Tens is a Scootle resource that works as an interactive place value chart. This particular resource is designed for students in year level 2, as students are required to challenge their understanding of place value in whole numbers up to 99. At the start of this game students receive a starting number, such as 86, and work towards turning it into a target number, such as 24, within the limit 20 turns.The overall purpose if this online activity is to try to achieve the target in as few turns as possible (Education Services Australia, 2016).
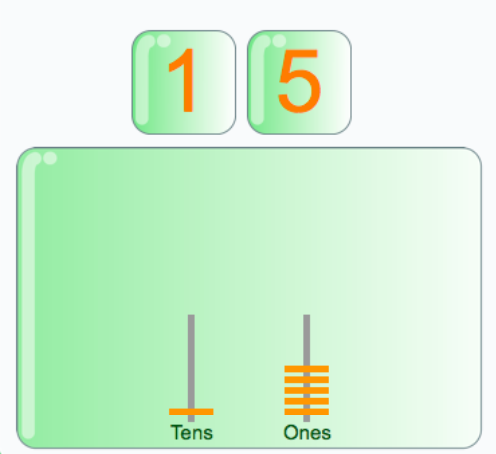
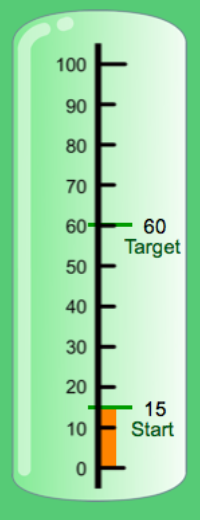
It would be smart to utilise this resource when students are at the mathematical stage of the language model, where students already understand the concept of place value, and are applying the skill of representing numbers up to 99.
Compared to similar resources, this resource cleverly displays numbers in various forms to make it easier for students to picture the outcome exapmples of this as shown above incoude a number line format, the number itself in symbolic form and a place value chart. This particular resource is 1 out of three that focus on different levels Wishball Challenge: Hundreds and Wishball Challenge: Thousands are two other versions designed for students that are ready to progress to using bigger units .
Resources or teaching strategies
This Place Value Abacus video is an easily accessible teaching resource used to demonstrate place value and help students gain a visual understanding of place holding within this system.
This video breaks down place value perfcctly and could be used for children from years 1 if dealing with smaller units or 2 upwards, mainly when students reach the mathematical stage of the language model. This would mainly be because they have not fully understood the concept of place value and require visual aids, and they are using the mathematical language of thousands, hundreds, tens, ones etc throughout the entireity of the video. This resource could be further developed and utilised in classroom to also show representations of decimals and the place value system of more complex places like tenths, hundredths etc to increase difficulty. Overall, the explanations throughout the video are simple enough to follow and replicate, while being effective for children to use individually to understand the skill of writing numbers in the correct place.
Textbook reading: one concept, skill or strategy
As discussed in the previous chapter, Reys starts chapter 8 with a recap stating “early number sense and counting naturally leads to place value as an organisational structure for number” (Reys, 2014). Backing up this statement he continues by explaining that the same principles for smaller numbers are involved as larger numbers are counted also. Representations no matter the type for larger numbers are still based on learning the pattern or sequence in a meaningful way to make concrete connections. Place value remains an important transition between symbols and language making it important to correctly model for students to avoid further misconceptions. Place value throughout all of students work links whole numbers, the 4 operations, the metric system and decimals (Reys, 2014).
References
Broadbent Maths. (2015). Place value – representation and misconceptions. Retrieved from https://www.broadbentmaths.com/pages/place_value__representation_and_misconceptions_255363.cfm
Education Services Australia. (2016). Wishball challenge: tens. Retrieved from http://www.scootle.edu.au/ec/viewing/L8459/L8459/index.html#
Jamieson-Proctor, R. (2019). EDMA241/262 Mathematics Learning and Teaching 1: Week 6 Part 2 (slide 3-7) Brisbane, Australia: Australian Catholic University.
Matholia. (2013, June 26). Place Value – Abacus [Video file]. Retrieved from https://youtu.be/QcpW-N_zHWk
Reys, R. E. (2014). Helping children learn mathematics 2e. Retrieved from https://ebookcentral-proquest-com.ezproxy1.acu.edu.au
Scootle. (2019). Home. Retrieved from https://www.scootle.edu.au/ec/p/home